Numerical and Theoretical Analysis of a New One-Dimensional Cellular Automaton Model for Bidirectional Flows
DOI:
https://doi.org/10.17815/CD.2024.151Keywords:
Pedestrian dynamics, Bidirectional flows, Cellular automatonAbstract
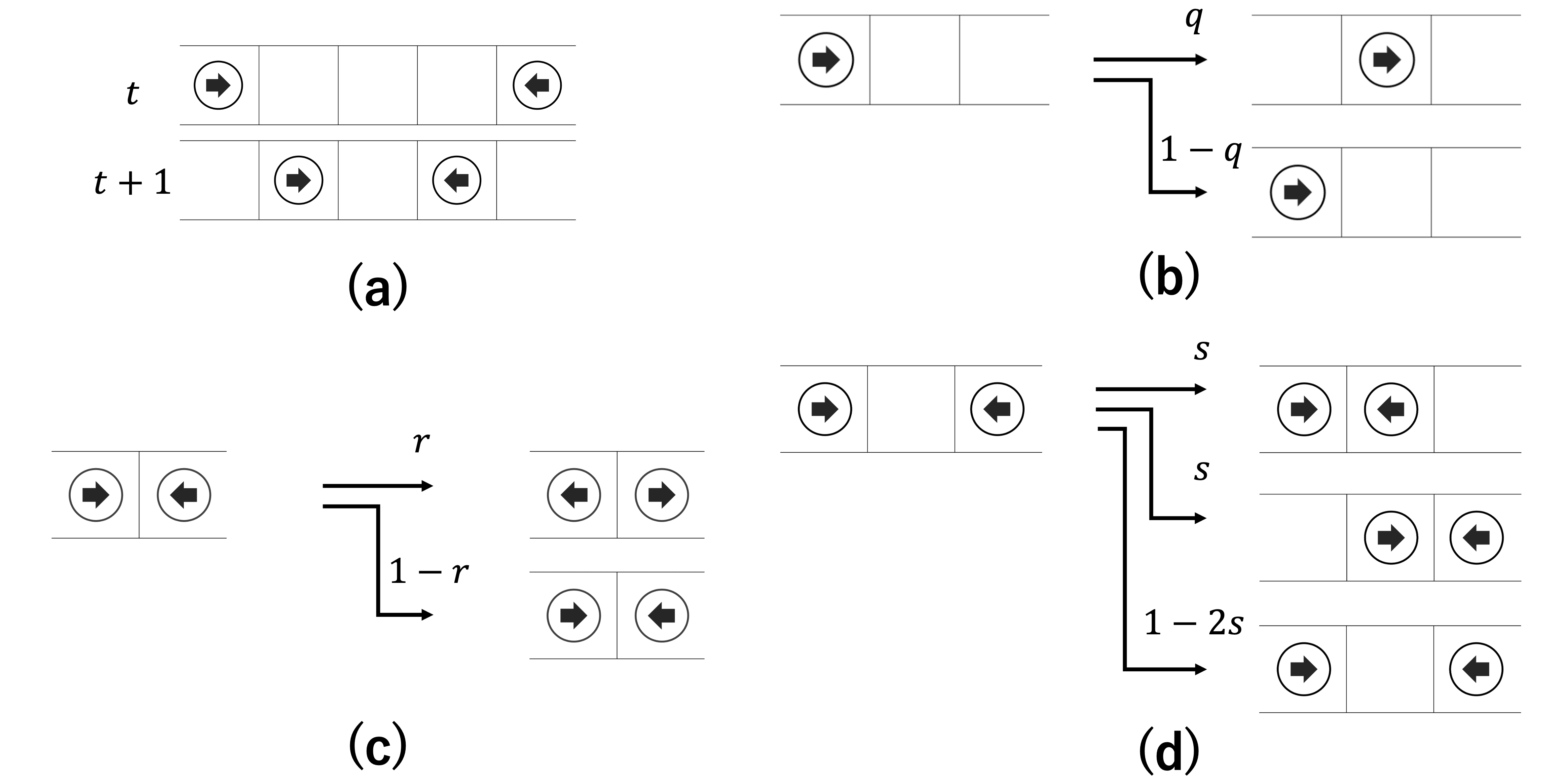
In recent years, research on mathematical models describing crowd dynamics has become increasingly important. Among this research, a two-dimensional mathematical model with the effect of body rotation describing bidirectional flows has been constructed, and its fundamental diagram has been shown to be qualitatively consistent with real experimental data from the perspective of flow rate inversion. However, this property has not been mentioned in one-dimensional mathematical models. In this paper, we introduce a new, simpler, one-dimensional cellular automaton model to focus on the direction of particles and the effect of flipping instead of body rotation by extending the well-known TASEP as a solvable lattice model. Our model was found to be qualitatively consistent with the actual phenomenon of flow rate inversion, both numerically and theoretically.
References
Schadschneider A., C.M.S.A.T.A., Zhang, J.: Pedestrian dynamics: From empirical results to modeling. Crowd Dynamics 1, 63-102 (2019). doi:10.1007/978-3-030-05129-7_4
Zhang J., K.W.S.A., Seyfried, A.: Ordering in bidirectional pedestrian flows and its influence on the fundamental diagram. J. Stat. Mech: Theory Exp. 2012(2), P02002 (2012). doi:10.1088/1742-5468/2012/02/P02002
Yanagisawa, D.: Coordination game in bidirectional flow. Collect. Dyn. 1, 1-14 (2016). doi:10.17815/CD.2016.8
Li Y., C.M.D.Z.Z.X.C.Y., Mebarki, A.: A review of cellular automata models for crowd evacuation. Physica A 526, 120752 (2019). doi:10.1016/j.physa.2019.03.117
Schadschneider A., C.A.N.K.: Stochastic Transport in Complex Systems From Molecules to Vehicles. Elsevier (2010). doi:10.1016/C2009-0-16900-3
Yamamoto H., Y.D.F.C., Nishinari, K.: Body-rotation behavior of pedestrians for collision avoidance in passing and cross flow. Transp. Res. Part B 122, 486-510 (2019). doi:10.1016/j.trb.2019.03.008
Murakami H., F.C.N.Y., Nishinari, K.: Mutual anticipation can contribute to self-organization in human crowds. Sci. Adv. 7, eabe7758 (2021). doi:10.1126/sciadv.abe7758
Evans M. R., F.D.P.G.C., Mukamel, D.: Spontaneous symmetry breaking in a one dimensional driven diffusive system. Phys. Rev. Lett. 74, 208-211 (1995). doi:10.1103/PhysRevLett.74.208
Downloads
Published
How to Cite
Issue
Section
Categories
License
Copyright (c) 2024 Kazuya Okamoto, Akiyasu Tomoeda

This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors contributing to Collective Dynamics agree to publish their articles under the Creative Commons Attribution 4.0 license.
This license allows:
Share — copy and redistribute the material in any medium or format
Adapt — remix, transform, and build upon the material
for any purpose, even commercially.
The licensor cannot revoke these freedoms as long as you follow the license terms.
Authors retain copyright of their work. They are permitted and encouraged to post items submitted to Collective Dynamics on personal or institutional websites and repositories, prior to and after publication (while providing the bibliographic details of that publication).








